地球の大きさを測る

概要

エラトステネスは紀元前に地球の大きさを求めた。 これは人類史に残る偉大な業績だが、隔たった2地点間の距離を別の方法で測る必要がある点で実用性に乏しい。 この記事では僕が最近考えついた、家から出ずに地球の大きさを測る方法を紹介する。

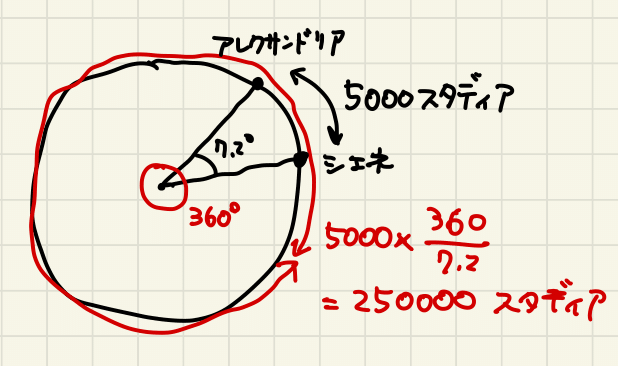
古代の学者エラトステネスは地球の大きさを計測した。 シエネとアレクサンドリアという二つの都市で太陽の南中高度が7.2度異なることから、2地点の緯度の差が円の1/50であるとわかる(図１)。 したがって都市の距離に50をかければ地球一周の大きさが求まる。 この話は高校の教科書とかで読んだ人も多いと思う。

今から2200年以上前にこの方法を実行できたのは様々な好条件に恵まれたからだ。

• 太陽と地球の距離は地球の大きさに比べて十分大きい。だから2地点にやってくる太陽光は平行であると近似してよい。
• シエネは北緯24度なので、夏至の正午に太陽がほぼ真上に来る。だからシエネとアレクサンドリアで同時に測定する必要はなく、アレクサンドリアで夏至の日に南中高度を調べればよい。
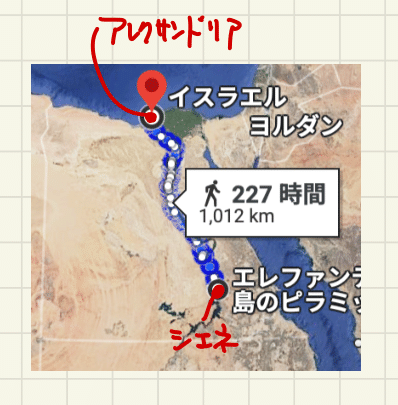
• シエネとアレクサンドリアはほとんど経度が等しい。だから2地点の距離をそのまま緯度方向の距離としてよい(図２)。
• シエネとアレクサンドリアの距離があらかじめ分かっていた。きっと古代エジプトから人の行き来が盛んだったんだろう。

僕はこの話が好きで、自分も地球の大きさを測りたいと前々から思っていた。 たとえば札幌と東京で同じ日に南中高度を測れば再現できるわけだけど、札幌-東京間の距離を地図で調べるのは負けた気がする。 遠く離れた2点間の距離を使わずに、できれば家から一歩も出ずに地球の大きさを測る方法はないだろうか？ エラトステネスの時代にはなかった技術と学問を使えばこれが達成できる。使うのはGPS衛星と万有引力の法則だ。

GPS衛星は非常に正確な時計を内蔵しており、その時計で測った衛星の時刻と衛星の現在位置を送信し続けている。 その信号を受信すれば、まず地表の時計と衛星の時計のずれ \(\Delta_t\) に光速 \(c\) を掛けて地表と衛星の距離 \(r_1 = c \times \Delta_t\) がわかる。 次に衛星の座標をしばらく受信すれば衛星の角速度 \(\omega\) がわかる。 衛星に働く重力と遠心力が釣り合っているので、万有引力の法則と衛星の角速度から地球の中心から衛星までの距離 \(r_2\) がわかる。

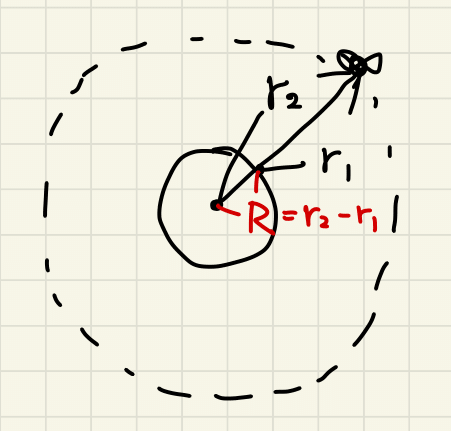
つまり \[ \begin{cases} m r_2 \omega^2 = G \frac{M m}{r_2^2} \\ m g = G \frac{M m}{R^2} \end{cases} \] より \[ r_2 = \left (\frac{g R^2}{\omega^2} \right )^{\frac{1}{3}} \] となる。 ここで \(M\) は地球の質量、\(m\) は衛星の質量、\(G\) は万有引力定数、\(g\) は地表面の重力加速度、\(R\) は地球の半径である。 最後に \(r_2-r_1\) を計算すれば地球の中心から地表までの距離、すなわち地球の半径 \(R\) がわかる(図３)。 (正確にいうと \(r_2\) を計算するのに \(R\) を使っているので、 \(R\) に関する閉じた式を解くことで \(R\) を求める必要がある。)

答えをカンニングして色々計算すると、この方法もやはり様々な好条件でうまくいくことがわかる。

• GPS衛星は24時間または12時間で地球を一周するので、地球の中心からの距離は4.3万kmないし2.7万kmだ。 これは地球の半径6300kmとおなじオーダーなので、 \(r_1\) と \(r_2\) の測定精度はそんなに高くなくていい。 万有引力定数と地球の質量と地球の大きさがたまたまちょうど良かったということだ。
• さらに、 \(\Delta_t\) は0.1秒オーダーなので、\(\Delta_t\) の測定もやはり簡単だ。 (もしこれがもっと小さかったら地表側にも高精度な時計が必要になる。) これは光速がちょうど良かったということだ。

ここまで分かればあとはやるだけだ。 スマホやカーナビなどGPS信号を受信する装置はそこらじゅうにあるが、GPS信号の中身を直接見るには専用の受信機が必要らしい。 このためだけにそれを買うのはもったいないので、誰か貸してくれませんか？

続きは測ったら書きます。