3周期はカオスを意味する

概要

LiとYorkeは、1975年の Period three implies chaosという題の論文で、離散力学系において3周期点が存在するならば任意の自然数の周期点が存在するというすごい定理を示した。 この記事ではその証明を解説する。

論文へのリンク

Li & Yorke, Period three implies chaos (1975)

背景

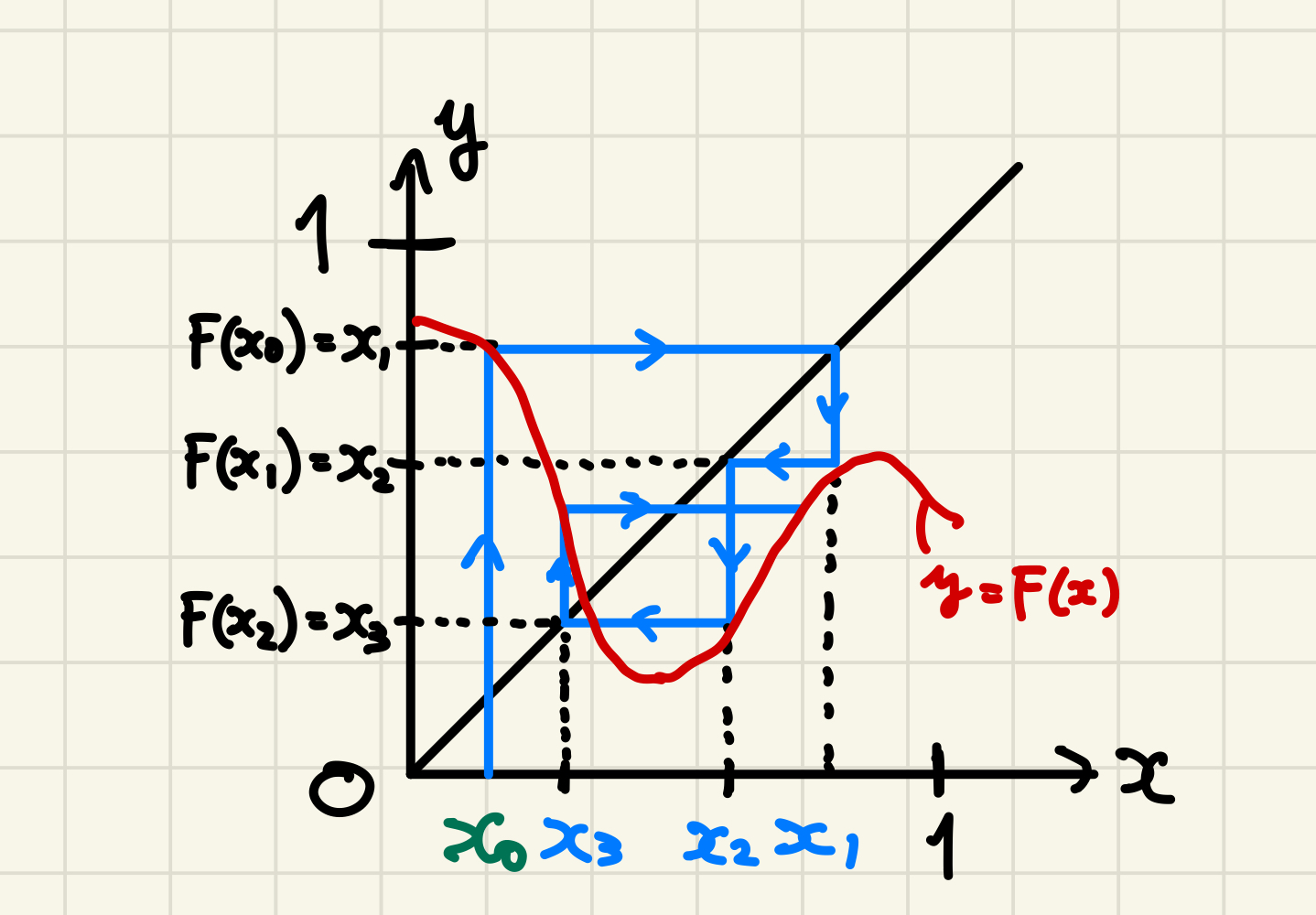
関数 $y = F(x)$ を考える。 ただし定義域は0以上1以下の実数で、値域も0以上1以下の範囲に含まれるとする。 このとき、ある初期値 $x_0 \in [0,1]$ から始めて $$ x_0, x_1 = F(x_0), x_2 = F(x_1), x_3 = F(x_2), ... $$ というように順次 $F$ を作用させた時系列 $\{x_t\}$ を考える。 これは例えば $F$ が今年のユスリカの個体数と来年のユスリカの個体数の関係を表す関数のとき、来年、再来年、3年後、...のユスリカの個体数を計算することに相当する。 図1に示すように、対角線で反射させると時系列が可視化できる。

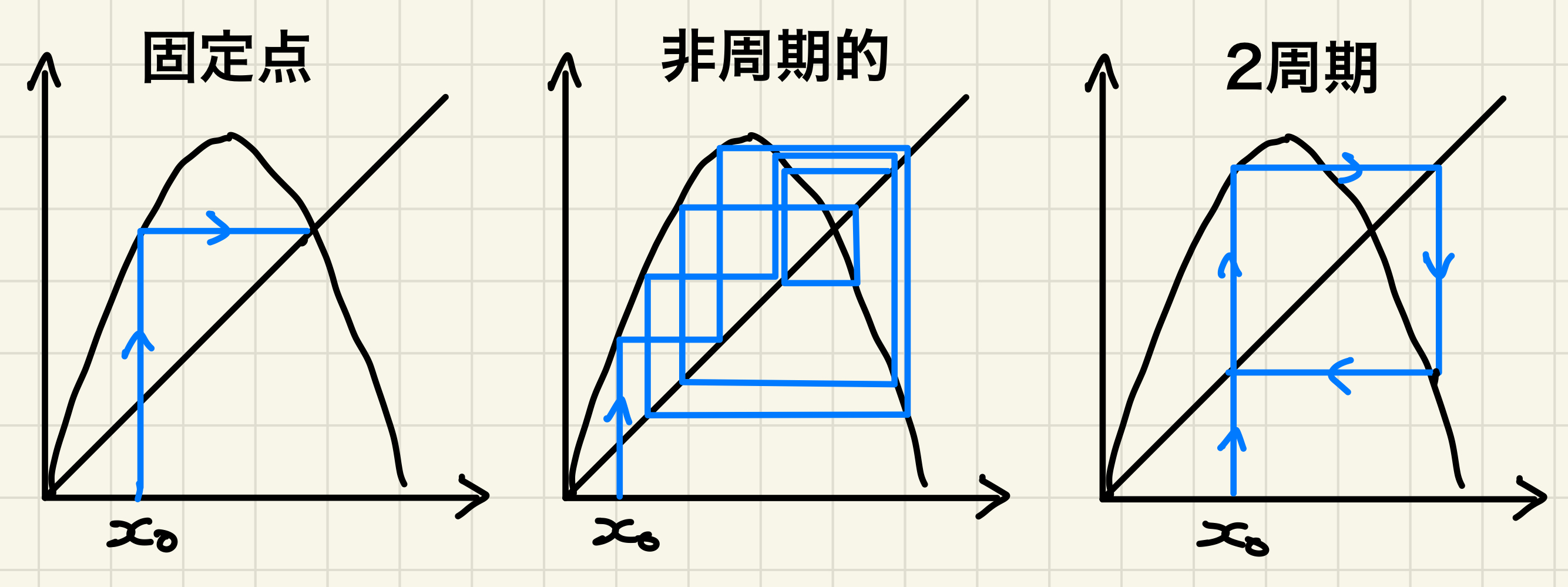
さて、ここで考えたいのは、この時系列がいつ周期的になるか？ その周期はいくつか？ という問題である。 手元で適当な $F$ を描いて対角線で反射させながらなぞってみよう。 ある初期値から始めると固定点（つまりグラフと対角線の交点）に落ちるかもしれない。 別の初期値から始めればずっと0から1までの間を不規則に行ったり来たりするかもしれない。 運が良ければ周期的な軌道（つまり有限個の点を順番に巡る軌道）に落ちるかもしれない。

このように、時系列の（非）周期性は関数 $F$ と初期値 $x_0$ に依存する。 つまり直感的には、同じ $F$ から生じる軌道でも、ある初期値からの軌道の性質によって別の初期値からの軌道の性質を調べることはできないと思える。 しかしLiとYorkeは、3周期点が存在するならば、任意の自然数の周期点が存在することを示した。

何がすごいのか？

• 上述のように、ある初期値からの軌道の情報で別の軌道の性質が調べられる
• 区間上で定義された任意の連続関数 $F$ について成り立つため、仮定が非常に弱い（一般性が高い）
• 3という数字が重要で、同じ証明は2でも4でも成り立たないので、なんか神秘的
• 実際に示している定理はより強力であり、実は3周期的である必要はない
• 元論文ではたったの1ページ半で簡潔に証明している

実際に示す定理

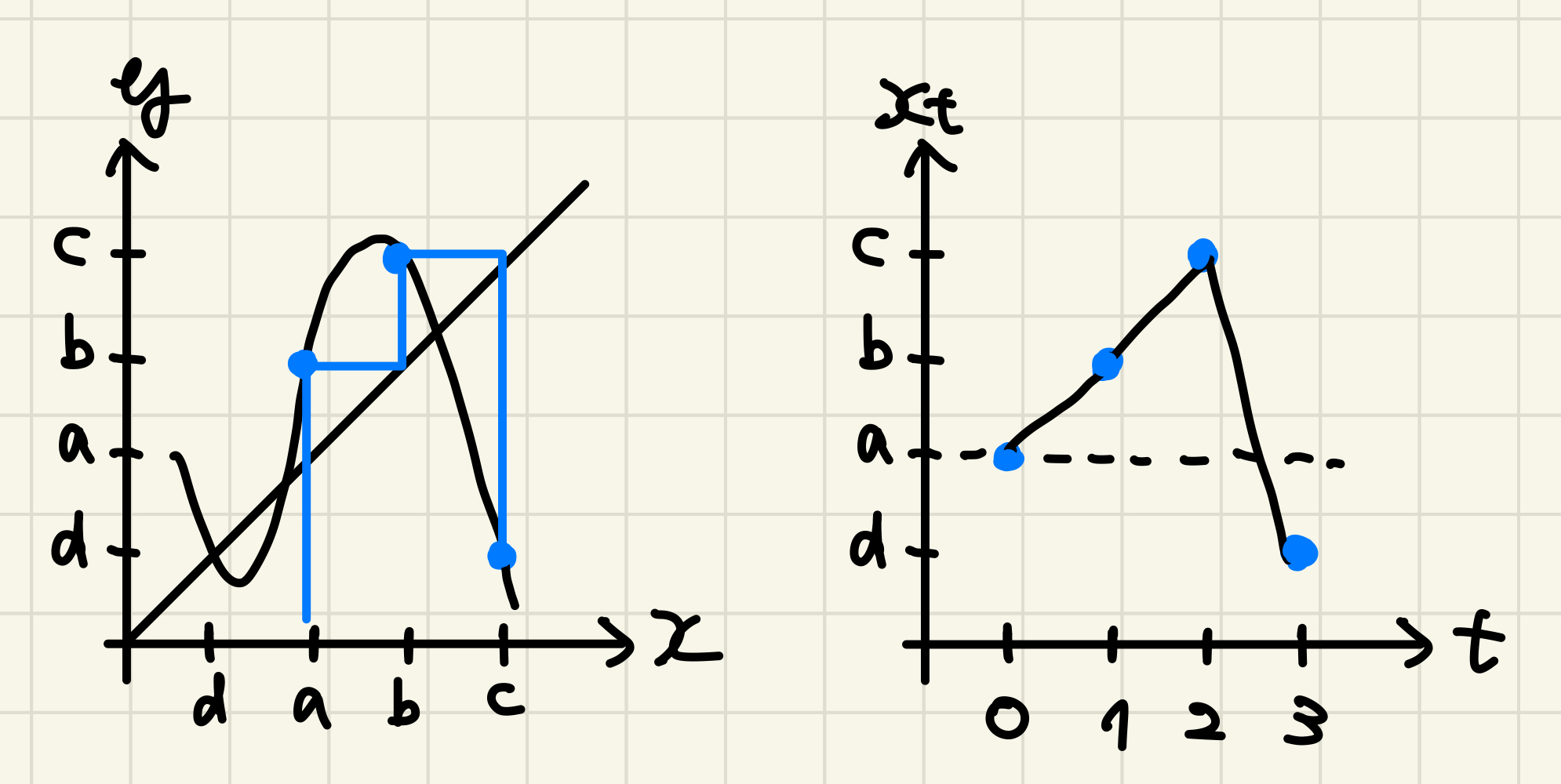
定理 区間 $J$ から $J$ への連続関数 $F$ を考える。 ある初期値 $a \in J$ から出発する軌道 $b = F(a), c = F(b), d = F(c)$ が $d \leq a < b < c$ （あるいは $d \geq a > b > c$ ）を満たすとき、任意の自然数 $k$ について $F$ の $k$ 周期点が存在する。

周期点の定義は次のとおり。
周期点 ある初期値 $x$ が ある自然数 $k$ について $F^k(x) = x$ かつ $ 1 \leq l < k$ を満たす任意の自然数 $l$ について $F^l(x) \neq x$ となるとき、$x$ は $F$ の周期 $k$ の周期点（あるいは $k$ 周期点）という。 後半の条件は、例えば単なる固定点を2周期点と呼ぶことを防ぐためである。

定理の条件が等号で成り立つとき、$a$ は3周期点である。 逆に、3周期点が存在するならば位相をずらすことで上の条件を満たす $a$ が必ず取れる。 したがって上の定理は、3周期点が存在するならば任意の周期の周期点が存在することを特別な場合として含んでいる。

証明の流れ

周期点の定義に従って、証明は次の2ステップで行う。

1. 任意の自然数 $k$ について、 $F^k(x) = x$ となる初期値 $x$ が存在することを示す
2. その初期値 $x$ が、$k$ より小さい自然数 $l$ で $F^l(x) \neq x$ を満たすことを示す

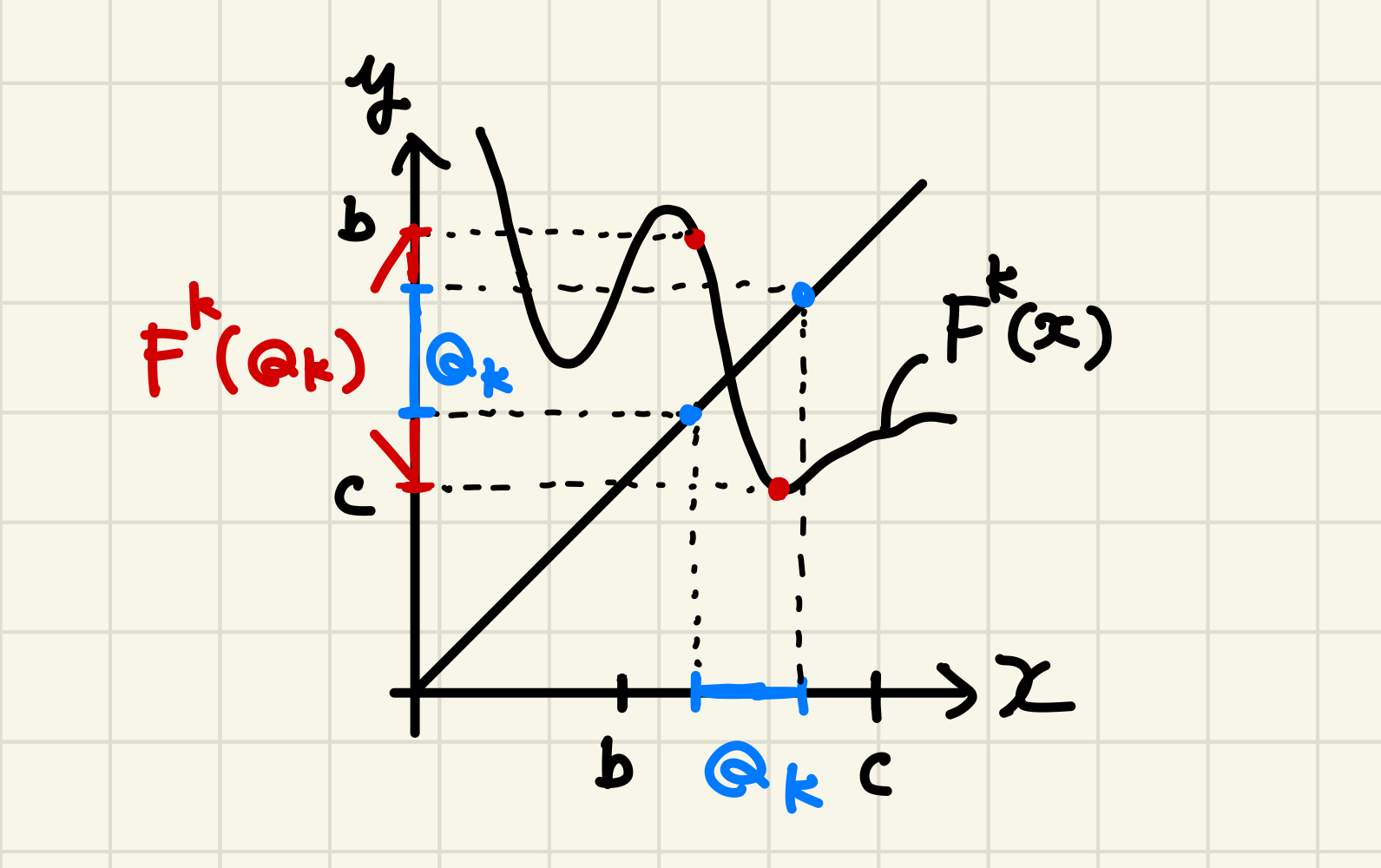
より具体的にいうと、任意の自然数 $k$ に対して、$F^k(Q_k) = [b,c]$ となる $Q_k \subset [b,c]$ が取れることを示す。 2.の証明はそのついでにできる。

証明

まず3つの補題を示して、次にそれを組み合わせて定理を示す。

補題0 $I$ を区間とし、$G: I \to \mathbb{R}$ を連続関数とする。 このとき任意の有界閉区間 $I_1 \subset G(I)$ について、$G(Q) = I_1$ となる有界閉区間 $Q \subset I$ が存在する。

証明（クリックして表示）

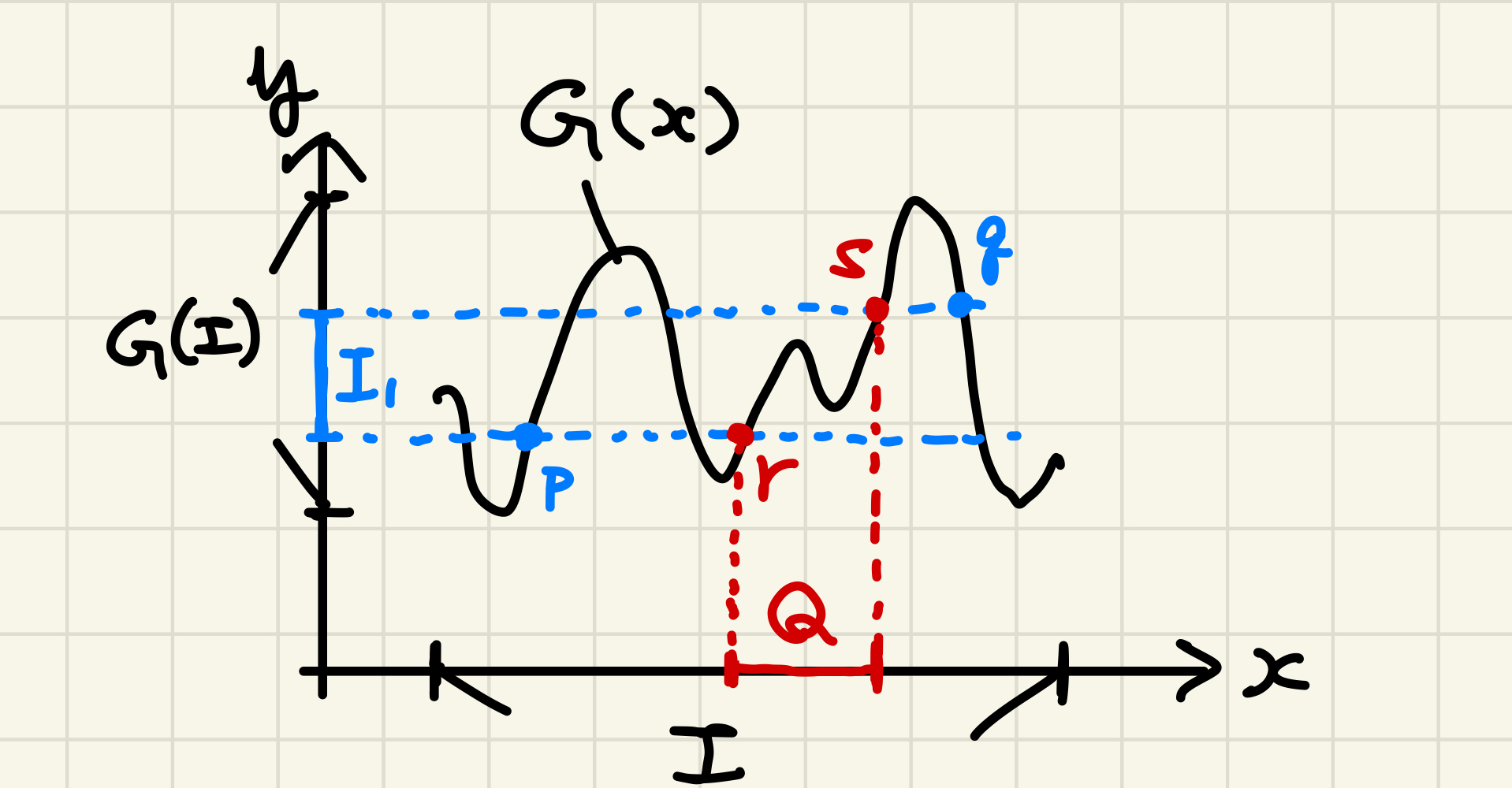
図のように $Q$ の端点 $r, s \in I$ を取ればOK。 $G$ は連続関数なので、$I_1$ の端点の逆像が $I$ に含まれる。 その中から１つずつ取ってきて $p, q$ とおく。 $p < q$ ならば、$r$ を下端の逆像のうち $q$ を超えない最大のもの、$s$ を上端の逆像のうち $r$ を下回らない最小のものとする。 $p > q$ の場合も同様。

補題1 $J$ を区間とし、$F: J \to J$ を連続関数とする。 有界閉区間の列 $\{I_n\}$ が任意の $n$ について $I_n \subset J$ かつ $I_{n+1} \subset F(I_n)$ を満たすとする。 このとき有界閉区間の列 $\{Q_n\}$ で、$Q_{n+1} \subset Q_n \subset J$ かつ $F^n(Q_n) = I_n$ を満たすものが存在する。

補題2（不動点定理） $J$ を区間とし、$G: J \to \mathbb{R}$ を連続関数とする。 $I \subset J$ を有界閉区間とする。 $I \subset G(I)$ のとき、$p=G(p)$ となる $p \in I$ が存在する。

証明（クリックして表示）

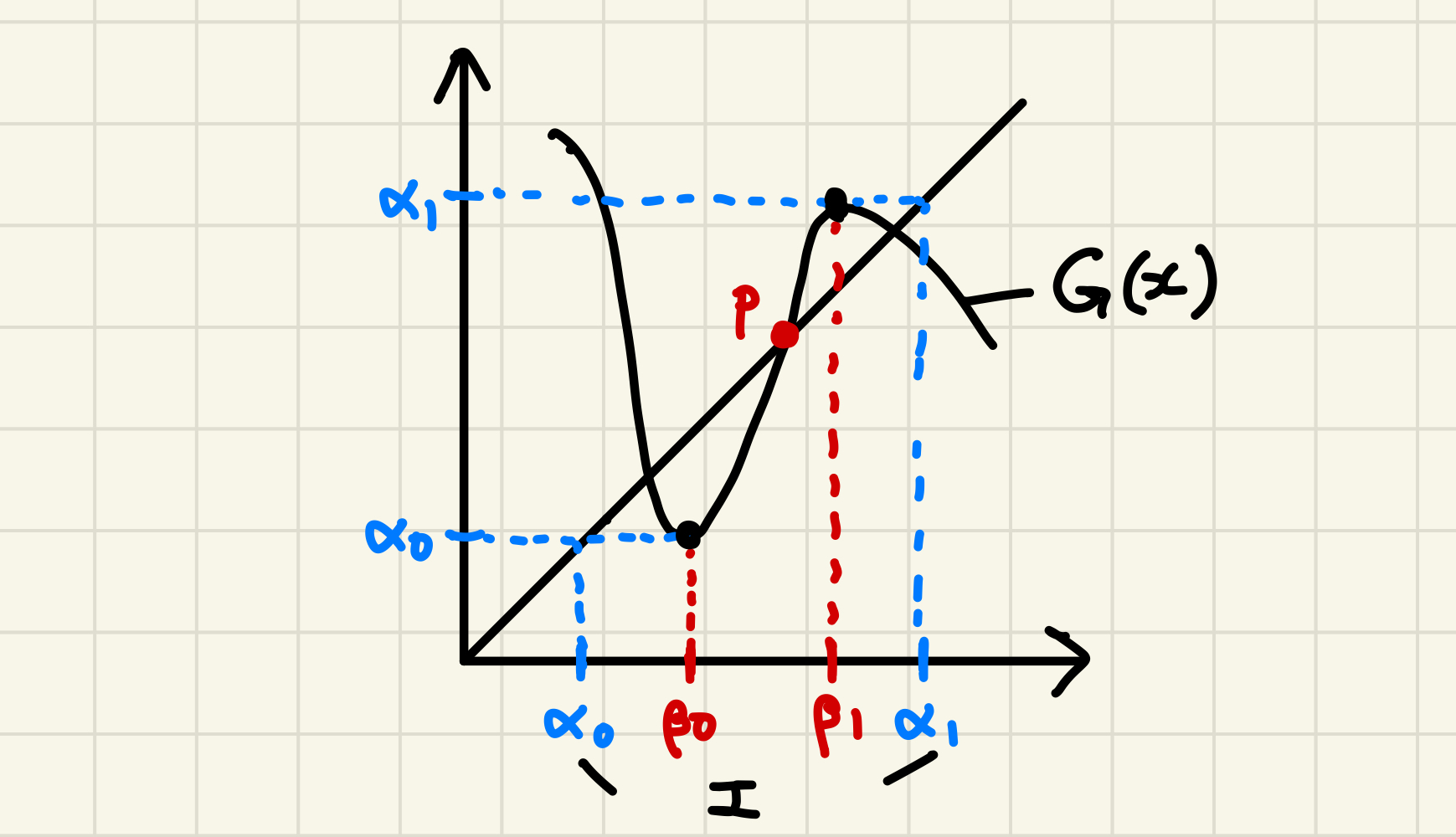
$I = [\alpha_0, \alpha_1]$ とおく。 $I \subset G(I)$ という仮定から $G(\beta_i) = \alpha_i$ となる点 $\beta_i \in I$ が取れる。 このとき $H(x) := x - G(x)$ は $H(\beta_0) \geq 0, H(\beta_1) \leq 0$ なので中間値の定理からある $p \in [\beta_0, \beta_1]$ で $H(p) = 0$ となる。 この $p$ が $G(p) = p$ となる点である。

それでは満を持して定理を証明しよう。ポイントは補題1を適用する区間の列 $\{I_n\}$ の取り方だ。

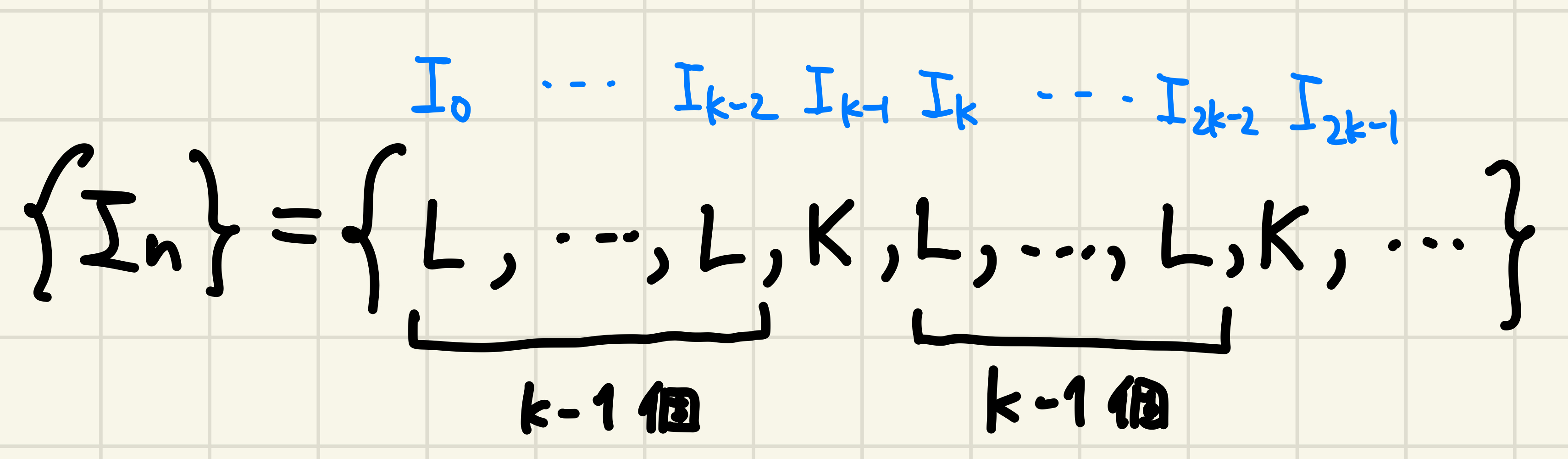
定理の証明 $L = [b,c], K = [a,b]$ とおく。任意の自然数 $k$ に対して、有界閉区間の列 $\{I_n\}$ を図7のように定める。 これは補題1の条件を満たすので、$Q_n \subset Q_{n-1} \subset J, F^n(Q_n) = I_n$ となる有界閉区間の列 $\{Q_n\}$ が取れる。 特に $Q_k \subset Q_0 = L = I_k = F^k(Q_k)$ なので、補題2より $p_k=F^k(p_k)$ となる $p_k \in Q_k$ が存在する。
  この $p_k$ が $l < k$ で $F^l(p_k) \neq p_k$ となることを背理法で示す。 もしある $l$ で $F^l(p_k) = p_k$ ならば、$F^{k-1}(p_k) \in K$ かつ $F^{k-1}(p_k) \in L$ であるため、$F^{k-1}(p_k) = b$ である。 よって $F^{k+1}(p_k) = d$ となり、これは $F^{k+1}(Q_k) = I_{k+1} = L$ に矛盾する。
  以上より $p_k$ は $k$ 周期点である。

おわりに

この記事ではLi&Yorke(1975)の証明を追った。 実はこの論文は決定論的な非周期軌道にカオスという名前を与えた初めての論文らしい。 上の定理以外にも、初期値鋭敏性を持つ非周期点の集合があることを示していたりと色々と面白いので、興味のある方は論文を読んでみてほしい。