マルチカノニカル法

概要

モンテカルロ法は、カノニカル分布における物理量の期待値を計算するのによく使われる。 通常の方法では温度が変わるとシミュレーションをやり直す必要がある。 この記事では、1回のシミュレーションだけで全ての温度での期待値を求められるマルチカノニカル法を説明する。

モンテカルロ法

モンテカルロ法とは、目的の確率分布 $P(x)$ に従う独立なデータ $X$ を大量にサンプルするためのアルゴリズムである。 例えば目的の確率分布としてカノニカル分布 $P(x) = \frac{e^{-\beta H(x)}}{Z}$ を考えよう。 もしもカノニカル分布に従うデータ $X$ が大量にサンプルできたなら、逆温度 $\beta$ での物理量 $A$ の期待値がサンプル平均で近似できる。 $$ \langle A \rangle_\beta = \frac{1}{Z}\sum_x A(x)e^{-\beta H(x)} \approx \frac1N\sum_{i=1}^{N} A(X_i) $$ 第1式における超高次元の和が、第2式ではサンプルについての和に化けている。 これによって数値計算が飛躍的に楽になる。

さて、上のようなサンプリングを実現するために、 $P(x)$ を定常分布にもつようなマルコフ過程を設計し、適当な初期分布から時間発展させるというのがモンテカルロ法のアイデアである。 各状態をとる確率のベクトル $v$ について、その更新則を $$ \begin{equation} v^{(k+1)} = Tv^{(k)} \end{equation} $$ と定める。定常状態 $v^*$ は $v = Tv$ の解である。これが目的の分布 $P(x)$ となればよい。 遷移行列 $T$ の各要素が正であれば、ペロン-フロベニウスの定理から唯一の定常状態に収束することが保証される（らしい）ので、そうなるように $T$ を設計するのがよい。

（注意：巨大なベクトル $v$ や超巨大な行列 $T$ を直接計算する（メモリに置く）わけではない。 実際に計算するのは状態の列 $\{X\}$ であり、これが $v$ に従うように状態 $X$ の更新則を定める。）

メトロポリス法によるカノニカルアンサンブル

メトロポリス法はモンテカルロ法を実現する方法の一つであり、おそらく最もよく使われている。 遷移行列 $T$ が分布 $v^*$ を定常分布にもつ条件は $$ \sum_y T_{xy}v^*_y = v_x^* : 釣り合い条件 $$ であり、その十分条件は $$ T_{xy}v^*_y = T_{yx}v_x^* : 詳細釣り合い条件 $$ である。 メトロポリス法では $T_{xy} := \mathrm{min} \left[ 1, e^{-\beta( H(x)- X(y))} \right] $ とする。 これによってカノニカル分布 $v_x^* = \frac{e^{-\beta H(x)}}{Z}$ に対して詳細釣り合い条件が成り立つ。

イジングモデル $H(x) = -J\sum_{i,j} x_ix_j -h\sum_i{x_i}$ を例にメトロポリス法の具体的なアルゴリズムを説明する。

1. 初期状態 $x_0$ を適当に定める
2. ランダムに一つのスピン $i$ を選び、反転した時のエネルギー変化 $\Delta E = 2x_i \left( J\sum_{j \in \partial i} x_j + h \right)$ を計算する
3. 確率 $\mathrm{min}\left[ 1, e^{-\beta\Delta E} \right] $ でスピン $i$ を反転する
4. 2と3を十分繰り返して、適当な間隔で状態を保存する

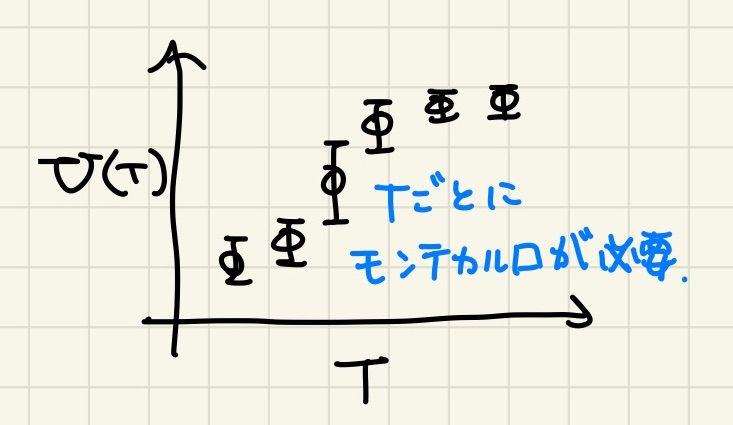
上のアルゴリズムでは $(T,h)$ を固定して計算していることに注意しよう。 例えば内部エネルギーの期待値 $U$ を $T$ の関数としてプロットするには、 $T$ を少しずつ変えて何度もモンテカルロシミュレーションを行う必要がある。

では、1回のシミュレーションで全ての $T$ について $U(T)$ を求めることはできるか？ マルチカノニカル法ならできる。

マルチカノニカル法によるカノニカルアンサンブル

マルチカノニカル法の本質は次の式変形である。 $$ \begin{align} \langle A \rangle_\beta &= \frac{1}{Z}\sum_x A(x)e^{-\beta H(x)} \\ &= \frac{1}{Z}\sum_x \sum_E \delta(H(x) - E)A(x)e^{-\beta H(x)} \\ &= \frac{1}{Z}\sum_E W(E)A(E)e^{-\beta E} \end{align} $$ ここで $A(E)$ はエネルギー $E$ を固定したときの $A$ の期待値、$W(E)$ はエネルギーが $E$ である状態の数（すなわちミクロカノニカル分布の状態数）である。

$A(E)$ と $W(E)$ を求める方法は以降の段落で説明することにして、これらが手に入ると何が嬉しいのかを先に説明する。 上の式変形で $\sum_x$ という超高次元の和が $\sum_E$ という1次元の和に置き換わっているので、 $$ \langle A \rangle_\beta = \frac{\sum_E W(E)A(E)e^{-\beta E}}{\sum_E W(E)e^{-\beta E}} $$ は四則演算だけで一瞬で計算できる。 好きな $T$ についてこの計算を行うことで、 $A$ が $T$ の関数として任意の細かさでプロットできる。 その精度は $A(E)$ と $W(E)$ の精度で決まるため、1度 $A(E)$ と $W(E)$ を高精度で求めておけば全ての $T$ について高精度で $\langle A \rangle_\beta$ が手に入る。

$A(E)$ と $W(E)$ を求めるために、まず $W(E)$ をワン-ランダウの方法で求める。 （実はこのステップでモンテカルロ法を10回くらい計算する必要があるが、それでもメトロポリスよりは断然速いし、自由エネルギーはメトロポリスでは求められないので、量的にも質的にもマルチカノニカル法の優位性は損なわれない。）

（カノニカル分布ではなく）重み $f(E(x))$ に従ってモンテカルロ法を実行する状況を考えよう。全てのエネルギー $E$ が等確率で出現する重み $f(E(x))$ は、 $$ f(E(x)) = \frac{1}{W(E)} = e^{-S(E)} $$ である。 逆にいうと、暫定的な $S(E)$ を用意して、エネルギー出現確率がフラットになるように $S(E)$ を更新すれば、これが収束したときに $S(E)$ はミクロカノニカル分布のエントロピー $S(E) = \log W(E)$ に一致している。 こうして $W(E)$ を求めるのがワン-ランダウの方法である。具体的なアルゴリズムは以下の通り。

1. $\eta = 1, S(E) = 0\, (\forall E)$ とする
2. $f(E(x)) = e^{-S(E)}$ の重みに従ってメトロポリス法を実行する
   つまり遷移確率を $\mathrm{min}\left[ 1, e^{-\Delta S(E)} \right] $ とする
3. あるエネルギー $E'$ が出現したら、そのエネルギーに対する重みを小さくするために $S(E') \leftarrow S(E') + \eta$ と更新する
4. 2と3をしばらく繰り返したら $\eta \leftarrow \frac{\eta}{2}$ で更新幅を小さくする
5. 2~4をしばらく(~10回)繰り返す

こうして $W(E)$ が手に入ったら、 $f(E(x)) = \frac{1}{W(E)}$ に従うメトロポリス法で全てのエネルギーが等確率で出るので、各エネルギーでの $A$ のサンプル平均 $A(E)$ も簡単に手に入る。

上のアルゴリズムで温度が登場しないことに注目しよう。必要なのはハミルトニアン $H(x)$ の情報だけだ。

再びイジングモデルの例に戻って、さまざまな物理量をマルチカノニカル法で求めてみよう。 以下では $N=400, h=0$ とする。

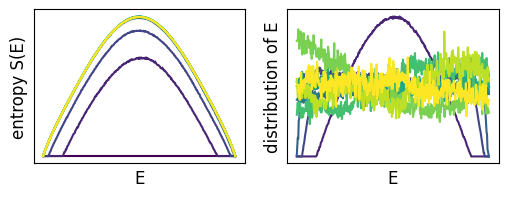
まずワン-ランダウの方法で $S(E)$ を計算する（図２）。 メトロポリス法を繰り返すにつれエントロピーが正確に求まり、エネルギーが一様に出現するようになっている。

次に物理量 $A$ として分配関数 $Z$ 、自由エネルギー $F$ 、内部エネルギー $U$ 、比熱 $C$ を計算する。 実はこれらの量は $A(E)$ の計算は不要である。 実際、

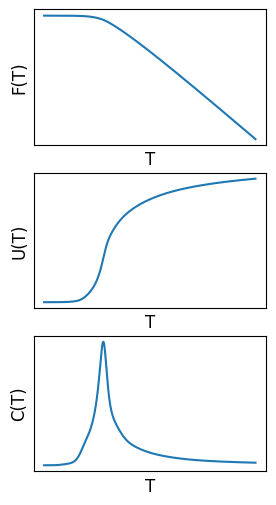
$$ \begin{align} Z(T) &= \sum_x e^{-\beta E(x)} \\ &= \sum_E e^{-\beta E} W(E) \end{align} $$ $$ \begin{align} F(T) &= -T \log Z(T) \\ &= -T \log \left( \sum_E e^{-\beta E} W(E) \right) \end{align} $$ $$ \begin{align} U(T) &= \frac{1}{Z} \sum_x e^{-\beta E(x)} E(x) \\ &= \frac{1}{Z} \sum_E e^{-\beta E} EW(E) \end{align} $$ $$ \begin{align} C(T) &= \frac{\langle E^2 \rangle - \langle E \rangle^2}{T^2} \\ &= \frac{1}{T^2} \left( \frac{\sum_E e^{-\beta E} E^2W(E)}{Z} - U^2(T) \right) \end{align} $$ という風に $W(E)$ だけから計算できる（図３）。

最後に非自明な $A(E)$ を用いる例として磁化を考える。

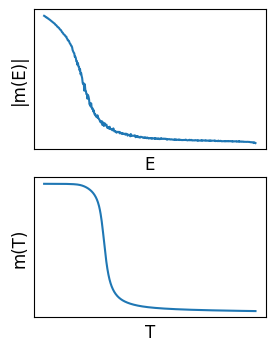
$$ \begin{align} m(T) &= \frac{1}{Z} \sum_x e^{-\beta E(x)} m(x) \\ &= \frac{1}{Z} \sum_E e^{-\beta E} W(E)m(E) \end{align} $$ なので、収束した重み $f(E(x)) = e^{-S(E)}$ を使って１回だけメトロポリス法を実行して $m(E)$ を求め、そこから $m(T)$ を求める（図４）。

以上の計算では、図2でワン-ランダウの方法を実行するのに4.6秒かかった。 図3は1次元の積分なので一瞬でできた。 図4は $m(E)$ を求めるメトロポリス法も $m(T)$ を求める積分も一瞬で終わった。

カノニカル分布では温度が固定されるので出現するエネルギーも制限される。 一方で温度を忘れたマルチカノニカル法ではエネルギーが一様分布で出現するので、相空間の珍しいところも巡ることができる。 したがって分布が多峰的であるときにメトロポリス法に対する優位性が顕著になると思う。