月の大きさを測る

概要

2025年9月8日は皆既月食が起きた。 この記事では月食の観測から月の大きさを測る方法を説明する。 特にアリスタルコスの有名な方法が実はうまくいかないということと、それを超える精度の方法を紹介する。

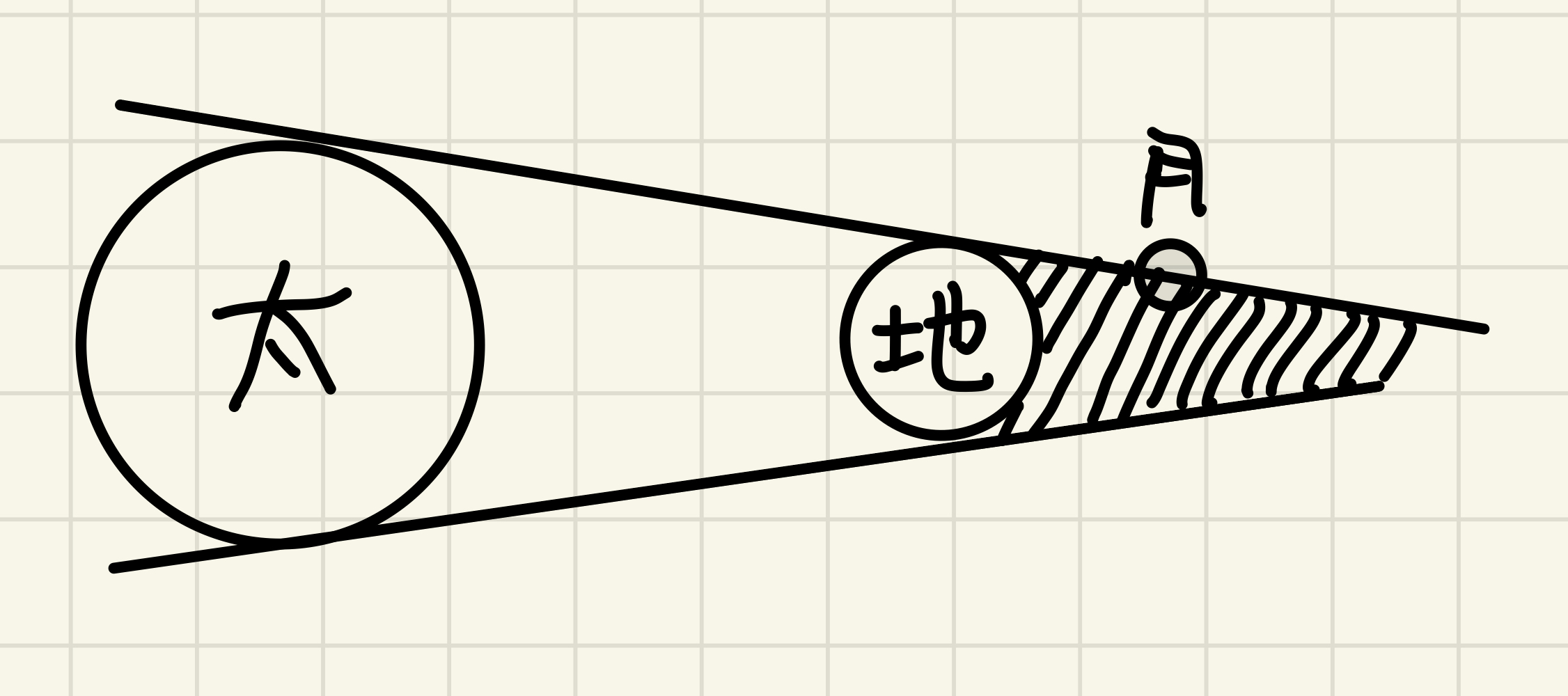
以前の記事で説明したように、人間は地球の大きさを測ることができる。 ところで月食とは月が地球の影に隠れる現象である。 ということは、地球の影の大きさと月の大きさを比べることで、月の大きさを測ることができる。 古代ギリシャのアリスタルコスも同じことを考えた。 よく知られた方法は図1の通りである。

しかしこの方法はうまくいかない。 実際の月の直径は約3476kmであり、誤差率は38%もある。 うまくいかない理由は、地球の影の大きさが地球の大きさと等しいという近似が成り立たないからだ(図2)。

実際に太陽までの距離、太陽の大きさ、月までの距離の文献値を使って地球の影の大きさを求めると9.28×10^3kmであり、月の直径は3.5×10^3kmと正しく推定される。 この補正の問題点はもちろん、各種の文献値を前もって知る必要があるということだ。 太陽と月の視野角を使えば必要な文献値の数は減らせるが、それでも太陽の直径(または太陽-地球間距離)の情報は必要だ。

ここからがこの記事の本題である。 地球の大きさ以外の文献値を使わずに、月の大きさを測ることはできるだろうか？ 以下3つの案を紹介する。

1.アリスタルコスの方法

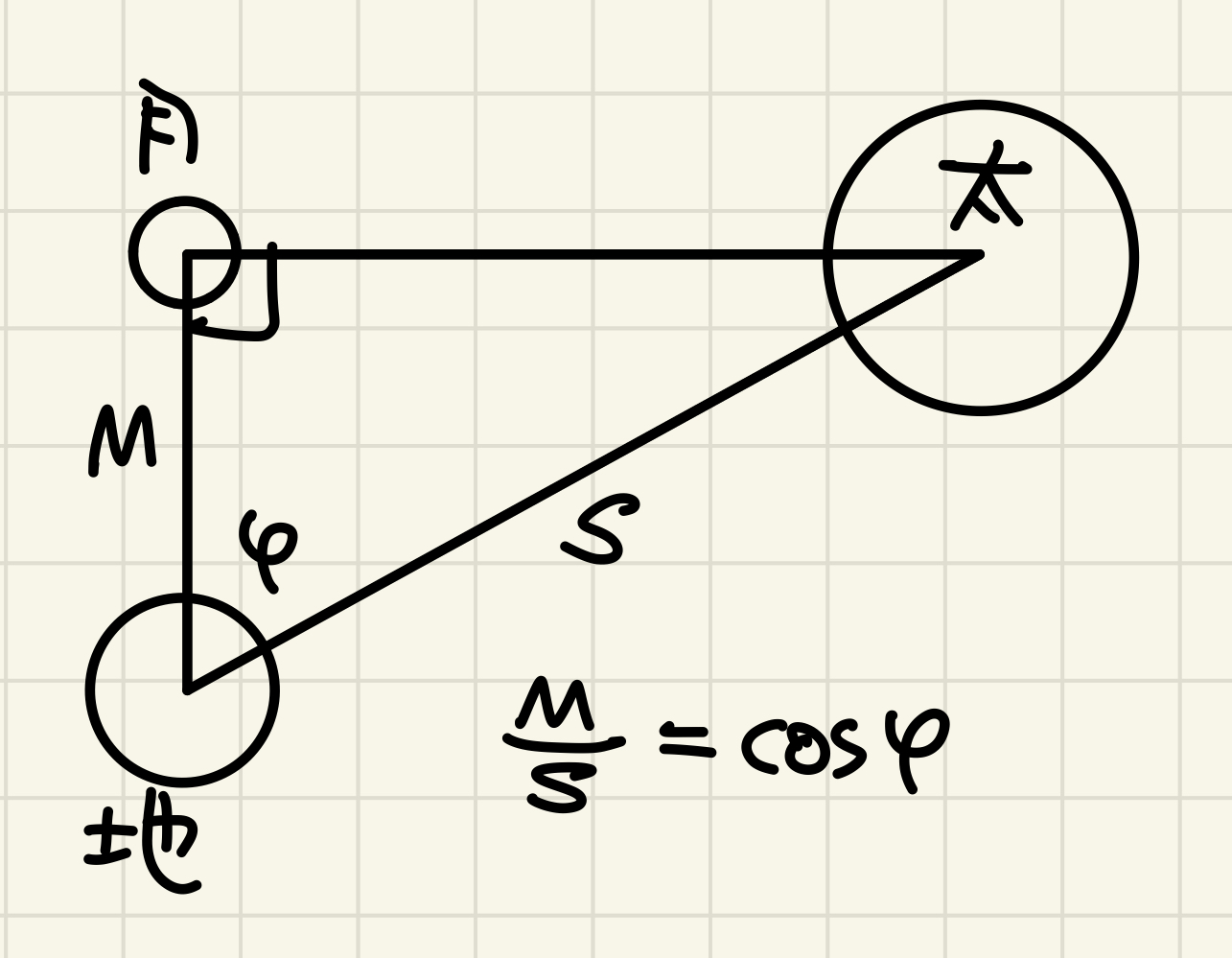
アリスタルコスのよく知られた方法は図1の通りで地球の影が平行であることを仮定したものだが、彼はさらに進んだ方法も考えていた。 それは半月の時の太陽と月の角度から太陽と月の距離の比を求める方法である(図3)。 この比がわかれば、視野角も使って月の直径を求めることができる。

この方法の問題点は角度の測定誤差に敏感であるということだ。 地球-太陽の距離 \(S\) は地球-月の距離 \(M\) に比べてかなり大きいので知りたい角度 \(\varphi\) はかなり90°に近い。 だから測定誤差が結果に大きく影響する。 実際、アリスタルコスは太陽までの距離が月までの距離の18倍から20倍だと推定したが、実際は390倍である。 19倍として計算すると月の直径は3.7×10^3kmとなり、誤差率は6.4%である。
参考：On the Sizes and Distances (Aristarchus)

2.T君の方法

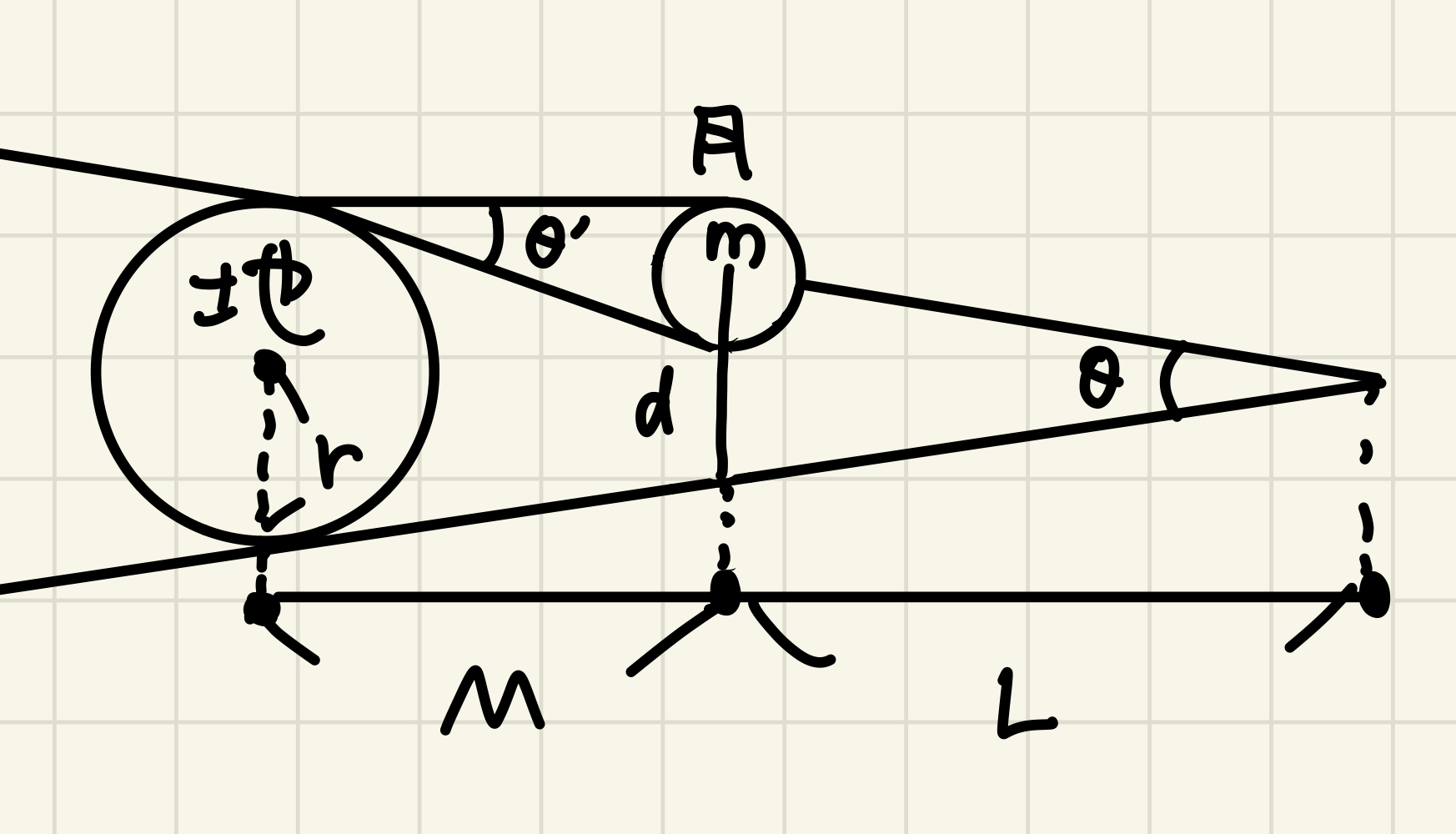
次に友達のT君が思いついた方法を説明する。 彼は太陽までの距離が月までの距離に比べ十分大きいことと、太陽と月の視直径が等しいことを仮定した。 このとき図4で次の3式が成り立つ。 \begin{cases} r = (M+L) \tan(\frac{\theta}{2}) \\ m = M \tan(\frac{\theta}{2}) \\ d = L \tan(\frac{\theta}{2}) \end{cases}

なんと \(\theta\) も \(M\) も \(L\) も消去できて、\(r = m(1+1/0.38)\) となる。 推定される月の直径は3.5×10^3kmで、誤差率は0.69%である。 図1の比率0.38と誤差率38%は偶然の一致ではなかったということだ。

3.半影の方法

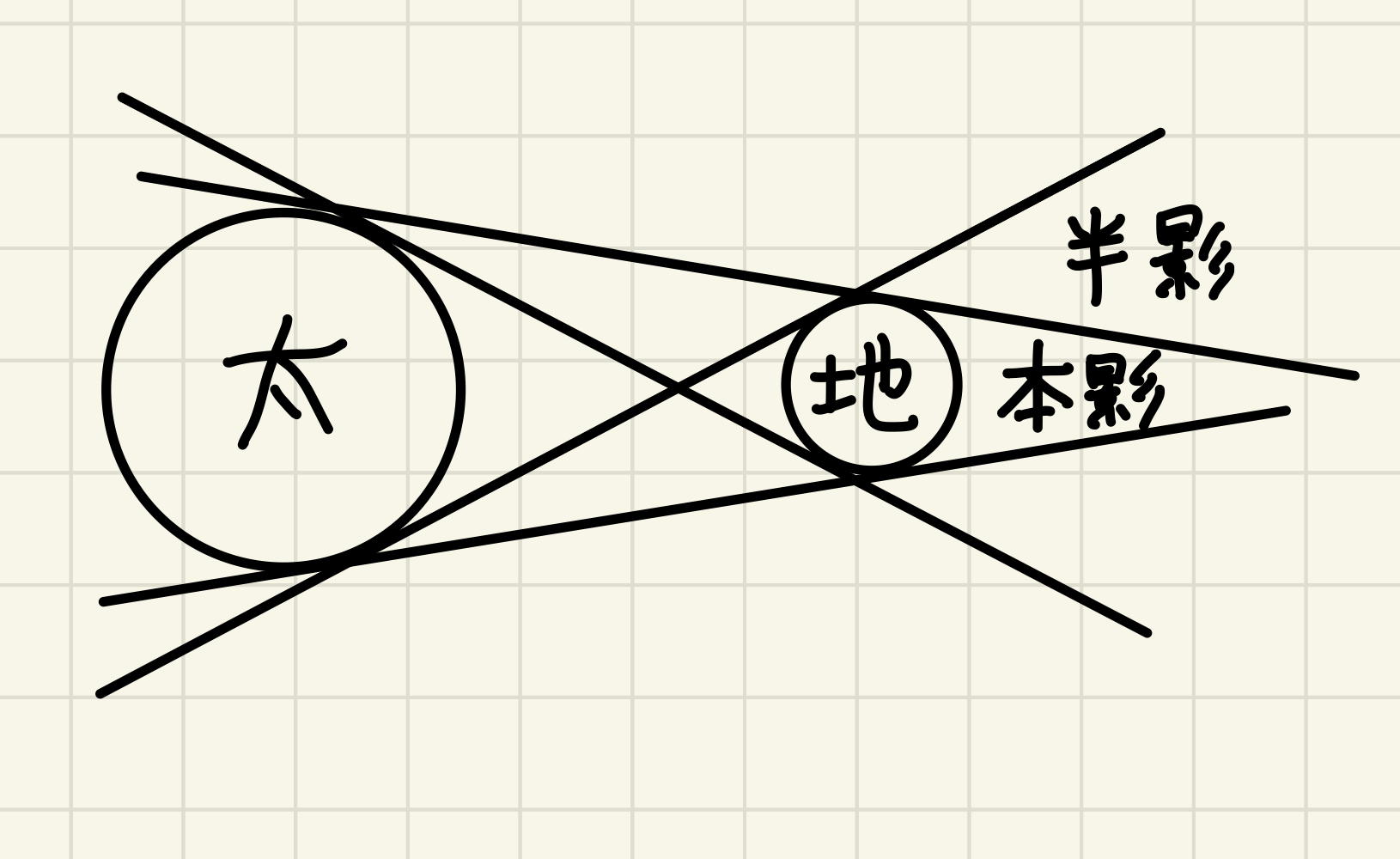
最後に僕が考えた方法を説明する。 上では省略していたが、地球の影には本影(太陽が完全に隠れる影)と半影(太陽が部分的に隠れる影)の２種類がある。 肉眼では本影しか見えないが、高感度のカメラなら半影の輪郭も見えると思う。 図1の方法か、あるいは月食中の通過時間を測ることで半影の大きさを求めれば、未知数二つで式が二つできて解けるはずだ。 この先はやってないのでわからない。

おまけ：太陽の大きさを求める

実は月食の情報を使わなくても、万有引力の法則を使えば月の大きさがわかる。 まず静止軌道の高さを \(R\) 、地球の半径を \(r\) とすると、力のつり合いから、 \[ \begin{cases} \frac{GMm}{R^2} = mR\omega^2 \\ \frac{GMm}{r^2} = mg. \end{cases} \] 1日が86400秒で重力加速度が9.81m/s^2であることを使って解くと、静止軌道の高さは \(R=4.23\times10^4\) kmとなる。 次に、ケプラーの法則と月の公転周期が27.3日であることから、 \[ \frac{M^3}{27.3^2} = R^3\\ \] すなわち月の軌道の高さは3.84×10^5kmとなる。 最後に月の視直径が0.525°であることを使って、月の直径は3.5×10^3kmとなる。 この方法の誤差率は0.69%である。

さて、こうして月の大きさ及び月までの距離を求めれば、月食の情報を使って今度は太陽の大きさを求めることができる。 (太陽の大きさがわかれば月の大きさがわかったように、月の大きさがわかれば太陽の大きさがわかるため。) こうして求めた太陽の大きさは直径1.8×10^6kmであり、実際の太陽の直径は1.392×10^6km(誤差率は29%)である。 計算の過程で、図3の近似がよく成り立つこと、すなわち太陽が月よりもずっと遠い天体だということが確認できる。